Riffle
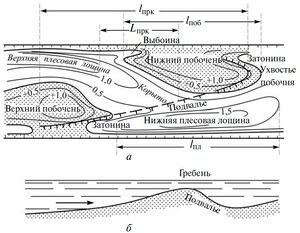
Перекат
Русла большинства рек характеризуются чередованием относительно мелководных участков большей или меньшей протяженности, в пределах которых рельеф русла представлен грядами разных размеров, и участков, отличающихся большими глубинами, выдержанностью их по длине реки, лишь изредка прерывающихся повышением отметок дна в связи с образованием отдельных крупных гряд. Первые из них называются перекатными; вторые — плесовыми. [2]
Определение на английском
Riffles exhibit higher water-surface slopes and faster velocities[3].
Пример использования термина на английском языке
We consider a generalized riffle shuffle on the colored permutation group and derive a determinantal formula for the probability of finding descents at given positions, proof of which is based on the bijection between the set of shuffles in question and that of non-intersecting lattice paths.[4]
Перевод использования на русском языке
Морфология перекатов как наиболее крупных форм рельефа русла, связанных с грядовым перемещением наносов, развитие которых определяется гидравлическими характеристиками потока. [5]
Список литературы
- ↑ Чалов Р. С. Толковый терминологический и понятийный словарь-справчник по русловедению. — Типография "Ваш формат". Москва, 2022. — 142 с.
- ↑ Чалов Р. С. Русловедение: Теория, География, Практика. Т. 2: Морфодинамика Речных Русел: Монография. М. : Красанд, 2011. 960 С,” 2013
- ↑ Stott T. Fluvial geomorphology // Progress in Physical Geography. – 2010. – Т. 34. – № 2. https://doi.org/10.1177/0309133309357284.
- ↑ Nakano F., Sadahiro T. Determinantal formula for generalized riffle shuffle // Discrete Mathematics. – 2021. – Т. 344. – № 12. https://doi.org/10.1016/j.disc.2021.112599.
- ↑ Чалов, Р. С., & Чалов, С. Р. (2020). Структурные уровни и морфодинамическая классификация русловых разветвлений. Водные Ресурсы, 47(3). https://doi.org/10.31857/s0321059620030049